Taylor and Francis Group is part of the Academic Publishing Division of Informa PLC

This site is operated by a business or businesses owned by Informa PLC and all copyright resides with them. Informa PLC's registered office is 5 Howick Place, London SW1P 1WG. Registered in England and Wales. Number 3099067.

Informa

Chapter 5: Exercises

Exercise 5.1

  1. Define “calculator” in today’s society. Give four different examples of calculators. Compare your list to a peer’s. Were you both thinking of calculators in the same way?
  2. Summarize and react to one article dealing with the use of calculators in a secondary mathematics classroom. Include all bibliographic information.

Exercise 5.2

  1. Name a mathematical concept that you feel would be hindered by the use of calculators and one that would be benefited by the use of calculators. Rationalize your position in both instances.
  2. How would you convince a student that memorization of basic fact tables is a convenience?

Exercise 5.3

  1. Devise a set of problems that could be used as a basis to teach the order of operations for addition, subtraction, multiplication, and division on the set of counting numbers. What is the impact of considering the whole numbers, integers, and reals on your discussion?
  2. Create a set of problems that could be used as a basis to teach the role of exponents and parentheses in the order of operations on the set of rational numbers.
  3. Is there any value to using larger numbers for the entries in the problem sets given to students as they are discovering the aspects of order of operations with their calculators or calculator applications? Why or why not?
  4. List the different sub-problems or readiness skills needed to explore
  5. 3 + (4 + 5[6 + 7 × 8] + 9) + 10 × 11 + 12.
  6. In part 4 of this exercise set only addition and multiplication were used. Discuss the advantages or disadvantages of avoiding subtraction and division. When should those operations be inserted into the developmental sequence and why? Where do exponents and roots enter the picture and why?

Exercise 5.4

  1. Discuss the advantages or disadvantages of selecting a sequence of exposures that lead students from excess in division being expressed as remainders, then fractions, and finally decimals.

Exercise 5.5

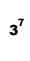  1. How does a calculator with a key deal with ÷ ? Describe how this information can be used to help students learn the laws of exponents. Does the calculator deal with 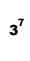÷ differently from ? If it does, what is the impact on its use as an instructional tool when having your students learn about the laws of exponents?
  2. In part 1 of this exercise, describe your response to a student asking about the difference between ÷ and where the base is not a prime number. Is the answer in terms of 4 or 2?
  3. Computers and calculators typically do not have commas or spaces between periods of numbers as we use in “standard” writing. Does dealing with values such as 2,417,851,639,229,258,349,412,352 without the commas create new problems for students? Why or why not?

Exercise 5.6

  1. Suppose you decide to provide an entry in the “missing factor” column of Table 5.1. Can the entries in the “number” and “sum of digits” columns be uniquely determined? Why or why not?
  2. Suppose you decide to provide an entry in the “sum of digits” column of Table 5.1. Can the entries in the “number” and “missing factor” column be uniquely determined? Why or why not?
  3. Devise a calculator routine that can be used for discovering the divisibility rule for 2. Establish a table similar to Table 5.1.
  4. To assist students in discovering the divisibility rule for 4, the third column of Table 5.1 needs to be changed to show the last two digits of the number being considered as divisible by 4. A similar table would be used for 8 except that the last column would show the last three digits of the number being considered. Devise a calculator routine that can be used for discovering the divisibility rule for 4 or for 8. Establish a table similar to Table 5.1 for the one you selected.
  5. Describe a calculator routine you would use to help students “discover” a divisibility rule for 6.

Exercise 5.7

  1. Create a lesson that uses the calculator to discover the Pythagorean theorem.
  2. Describe two unrelated situations in which a calculator would be a useful tool in assisting a student to learn a concept from geometry.

Exercise 5.8

  1. Summarize the contribution to gambling theory made by a mathematician or technology from some decade.
  2. Report on the role mathematicians played in the development of a topic. For example, how did the needs of surveyors impact the development of trigonometry?

Exercise 5.9

  1. Create a lesson dependent on a graphing calculator. Do it on two different graphing calculators. Describe the advantages and disadvantages of each of the selected calculators. Does your bias show in the description?
  2. Create a lesson dependent on dynamic geometry capabilities. Do it on a TI-92, TI-89, Casio Classpad, or CFX-9850G. Describe your reactions and feelings.
  3. How do you enter a circle centered at the origin with a radius of 2 into your graphing calculator in order to graph it? Describe the limitations, special considerations, and added knowledge the student would need to possess to do this problem.

Exercise 5.10

  1. Summarize and react to one article dealing with the use of computers in a secondary mathematics classroom. Include all bibliographic information.
  2. Summarize and react to one article dealing with the use of technology other than calculators or computers in a secondary mathematics classroom. Include all bibliographic information.
  3. Identify five different software packages for symbolic manipulation/function plotting on a computer. Investigate at least two of these applications. Summarize the capabilities of each piece. Describe any unique features of each product. Compare and contrast the software, selecting the one you feel would be most beneficial in the classroom.
  4. Investigate at least two different selections of dynamic geometry software available today. Summarize the capabilities of each piece. Describe any unique features of each product. Compare and contrast the software, selecting the one you feel would be most beneficial in the classroom.
  5. Use a symbolic manipulator/function plotting software package to find the value of ,,,, etc. How large a number will the software allow before the answer cannot be determined? Select another piece of software and repeat the activity. Did you get the same results?

Exercise 5.11

  1. Identify five applications for the mathematics classroom that can be installed on a hand-held device such as an iPhone, Galaxy Nexus, iPad, Xoom, XY Board, Tab, or Kindle Fire. Rank order these applications for student learning value in the secondary mathematics curriculum. Justify your ranking. 

Exercise 5.12

  1. Do you think purchasing a notebook computer as a college requirement is a viable solution to getting computers into the mathematics classroom? Why or why not?
  2. Do you think purchasing a tablet computer such as an iPad, Xoom, or Galaxy Tab as a college requirement is a viable solution to getting technology into the mathematics classroom? Why or why not?
  3. Should students be required to use the same software (calculator) that is used for demonstration purposes? Why or why not?
  4. Which of the software (calculators) you have used can be used in the mathematics classroom? Are there other pieces of software you should investigate as a potential tool in the classroom? Why or why not?

Exercise 5.13

  1. E-mail a challenging problem to a fellow educator or teacher-to-be. Make sure you request a response. Judge the answer and send back a reply explaining your reasoning.

Exercise 5.14

  1. Find an Internet site that can be used for secondary mathematics. Develop a lesson plan using that site.
  2. Locate the Ole Miss Math Challenge at http://mathcontest.olemiss.edu. Try the current week’s problem for either the Problem of the Week or Algebra in Action. Your goal is to get your name added to the site. What number on the list did you achieve?

Exercise 5.15

  1. Create a 5 - 8 minute video to teach a specific math concept. Show the video to a peer and ask for feedback. Show the video to a student and ask for additional feedback. Use the feedback from your peer and the student to remake the video. Share the video on a site for the world to see. How do you feel about your product? 

Chapter 5: Problem Solving Challenges

 

Question 1

How many retangles of any size are on an 8 x 8 chessboard?

Answer    [Click to reveal...]

Answer: 1296

On a 1 x 1 chessboard, there is only 1 rectangle. On a 2 x 2 chessboard, there are 9 rectangles (4 small 1 x 1 squares, 1 large 2 x 2 square and 4 1 x 2 rectangles)

On a 3 x 3 chessboard, there are 36 rectangles (9 small 1 x 1 squares, 1 large 3 x 3 square, 4 2 x 2 squares, 6 1 x 3 rectangles, 12 1 x 2 rectangles, 4 2 x 3 rectangles).

Notice that the values are perfect squares of triangular numbers.

  • 1 x 1    1st triangular number 1^2 or 1 rectangle
  • 2 x 2    2nd triangular number 3^2 or 9 rectangles
  • 3 x 3    3rd triangular number 6^2 or 36 rectangles
  • 4 x 4    4th triangular number 10^2 or 100 rectangles
  • 5 x 5    5th triangular number 15^2 or 225 rectangles
  • 6 x 6    6th triangular number 21^2 or 441 rectangles
  • 7 x 7    7th triangular number 28^2 or 784 rectangles
  • 8 x 8    8th triangular number 36^2 or 1296 rectangles

 

 

Question 2

If it takes 10 sheep ten minutes to jump over a fence one at a time, how many sheep could jump over the fence in one hour?

Answer    [Click to reveal...]

Answer: 55

The interval between jumps for 10 sheep in ten minutes is 10/9 of a minute. The intervals between the first sheep and the tenth would be 10 divided by 10/9 = 9 intervals for 10 sheep. In other words, with 10 sheep, there are only 9 intervals between jumps where each interval is 10/9 of a minute. In 60 minutes 60 divided by 10/9 = 54 intervals in one hour producing 55 sheep in one hour over the fence.

Chaper 5: Videos

 

Introduction

Sticky Question

Problem Solving